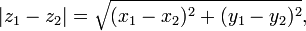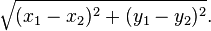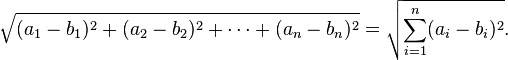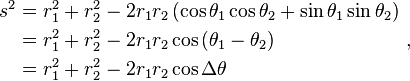Versão 1.0
Em matemática , o teorema de Pitágoras é uma relação na geometria euclidiana entre os três lados de um triângulo retângulo. Em termos de áreas, ele afirma:
Em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa (o lado oposto ao ângulo recto) é igual à soma das áreas dos quadrados cujos lados são as duas pernas (os dois lados que se encontram numa ângulo direito ).
O teorema pode ser escrita como uma equação relacionando os comprimentos dos lados a , b e c , chamado frequentemente a equação de Pitágoras:
onde c representa o comprimento da hipotenusa, e um e b representam os comprimentos dos outros dois lados.
O teorema de Pitágoras é nomeado após o grego matemático Pitágoras , que por tradição é creditado com a sua descoberta e prova, embora seja frequentemente argumentado que o conhecimento do teorema é anterior a ele. Há evidências de que os matemáticos Babilônia desenvolveu a fórmula, embora haja pouca evidência sobrevivente que utilizou em uma estrutura matemática.
O teorema tem inúmeras provas , possivelmente mais do que qualquer teorema matemático. Estes são muito diversificados, incluindo tanto as provas geométricas e algébricas provas, com alguns milhares de anos atrás. O teorema pode ser generalizado de várias maneiras, incluindo dimensões superiores espaços, em espaços que não são euclidiana, a objetos que não são triângulos retângulos, e de fato, a objetos que não são triângulos em tudo, mas n -dimensionais sólidos. O teorema de Pitágoras atraiu o interesse fora da matemática como um símbolo de hermetismo matemática, mística, ou o poder intelectual; referências populares da literatura, peças teatrais, musicais, músicas, selos e desenhos animados abundam.
triplos de Pitágoras
A tripla pitagórica tem três números inteiros positivos de um , b , e c , de tal forma que um 2 + b 2 = c 2 . Em outras palavras, uma tripla pitagórica representa os comprimentos dos lados de um triângulo retângulo, onde os três lados têm comprimentos inteiros. A evidência de monumentos megalíticos da Europa do Norte mostra que triplica tais eram conhecidos antes da descoberta da escrita. Tal é geralmente escrita triplo ( um , b , c ). Alguns exemplos bem conhecidos são (3, 4, 5) e (5, 12, 13).
A primitiva de Pitágoras triplo é aquele em que um , b e c são primos entre si (o maior divisor comum de um , b e c é 1).
O seguinte é uma lista de primitivas trios pitagóricos com valores inferiores a 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12 , 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77 , 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
comprimentos incomensuráveis
Uma das consequências do teorema de Pitágoras é que os segmentos de linha cujos comprimentos são incomensuráveis (por isso o rácio de que não é um número racional ) pode ser construído usando uma régua e um compasso . Teorema de Pitágoras permite a construção de comprimentos incomensuráveis porque a hipotenusa de um triângulo está relacionado com os lados pela raiz quadrada de operação.
A figura da direita mostra como a construção de segmentos de linha, cujos comprimentos estão na relação de raiz quadrada de qualquer número inteiro positivo. Cada uma tem um lado do triângulo (identificado como "1"), que é a unidade escolhido para a medição. Em cada um triângulo retângulo, o teorema de Pitágoras estabelece o comprimento da hipotenusa em termos de unidade. Se uma hipotenusa está relacionada com a unidade da raiz quadrada de um número inteiro positivo, que não seja um quadrado perfeito, é a realização de um comprimento incomensurável com o aparelho, tais como √ 2 , √ 3 , √ 5 . Para mais detalhes, consulte Quadrática irracional .
Comprimentos incomensuráveis em conflito com o conceito da escola pitagórica de números como apenas números inteiros. A escola pitagórica tratado com proporções por comparação de múltiplos inteiros de uma subunidade comum. De acordo com uma lenda, Hippasus de Metaponto ( ca. 470 aC) foi afogado no mar para dar a conhecer a existência do irracional ou incomensuráveis.
Os números complexos
Para qualquer número complexo
o valor absoluto ou módulo é dada pela
Assim, as três quantidades, r , x e y estão relacionados pela equação de Pitágoras,
Note-se que r é definido como um número positivo ou zero, mas x e y pode ser negativo, bem como positivo. Geometricamente r é a distância entre a z a partir de zero ou de origem O do plano complexo .
Isso pode ser generalizado para saber a distância entre dois pontos, z 1 e z 2 dizer. A distância requerida é dado pela
portanto, novamente eles estão relacionados por uma versão da equação de Pitágoras,

distância euclidiana em vários sistemas de coordenadas
A fórmula de distância em coordenadas cartesianas é derivado do teorema de Pitágoras. Se ( x 1 , y 1 ) e ( x 2 , y 2 ) são os pontos no plano, em seguida, a distância entre eles, também chamada a distância Euclidiana , é dado pela
De modo mais geral, em euclidiana n -espaço , a distância euclidiana entre dois pontos, 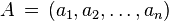 e
e  , é definida, pela generalização do teorema de Pitágoras, como:
, é definida, pela generalização do teorema de Pitágoras, como:
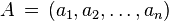 e
e  , é definida, pela generalização do teorema de Pitágoras, como:
, é definida, pela generalização do teorema de Pitágoras, como:
Se as coordenadas cartesianas são não usada, por exemplo, se as coordenadas polares são utilizados em duas dimensões, ou, em termos mais gerais, se coordenadas curvilíneas são usados, as fórmulas expressando a distância Euclidiana é mais complicado do que o teorema de Pitágoras, mas pode ser derivado a partir de lo. Um exemplo típico em que a distância em linha recta entre dois pontos é convertida em coordenadas curvilíneas pode ser encontrada nos pedidos de polinómios de Legendre na física . As fórmulas podem ser descoberto usando o teorema de Pitágoras com as equações relativas coordenadas curvilíneas em coordenadas cartesianas. Por exemplo, as coordenadas polares ( r , θ ) pode ser introduzida como:
Em seguida, dois pontos com localizações ( r 1 , θ 1 ) e ( r 2 , θ 2 ) estão separados por uma distância s :
Realizando as praças e os termos que combinam, a fórmula de Pitágoras para a distância em coordenadas cartesianas produz a separação em coordenadas polares como:
usando as funções trigonométricas produto para soma-fórmulas . Esta fórmula é a lei dos co-senos , algumas vezes chamado o Teorema de Pitágoras Generalizada. A partir deste resultado, para o caso em que os raios para os dois locais são perpendiculares, o ângulo fechado ô q = π / 2, e de forma a correspondente ao teorema de Pitágoras é recuperado: 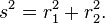 O teorema de Pitágoras, válido para triângulos retângulos, portanto, é um caso especial da lei mais geral dos cossenos, válido para triângulos arbitrários.
O teorema de Pitágoras, válido para triângulos retângulos, portanto, é um caso especial da lei mais geral dos cossenos, válido para triângulos arbitrários.
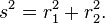 O teorema de Pitágoras, válido para triângulos retângulos, portanto, é um caso especial da lei mais geral dos cossenos, válido para triângulos arbitrários.
O teorema de Pitágoras, válido para triângulos retângulos, portanto, é um caso especial da lei mais geral dos cossenos, válido para triângulos arbitrários.Pitágoras trigonométrica identidade
Em um triângulo retângulo com os lados um , b e hipotenusa c , trigonometria determina o seno e co-seno do ângulo θ entre o lado de um ea hipotenusa como:
Do que se segue:
onde o último passo aplica-se o teorema de Pitágoras. Esta relação entre o seno e co-seno, por vezes, é denominado a fundamental de Pitágoras identidade trigonométrica. Em triângulos semelhantes, as razões entre as partes são as mesmas, independentemente do tamanho dos triângulos, e dependem dos ângulos. Consequentemente, na figura, o triângulo com hipotenusa do tamanho da unidade tem lado oposto do tamanho sin θ lado e adjacentes de tamanho cos θem unidades da hipotenusa.
Relação com o produto vetorial
O teorema de Pitágoras relaciona o produto cruzado e produto escalar de uma forma similar:
Isto pode ser visto a partir das definições de produto cruzado e produto escalar, como
com n um vector unitário normal a ambos um e b . A relação segue a partir dessas definições e da identidade de Pitágoras trigonométrica.
Isto também pode ser utilizado para definir o produto cruzado. Rearranjando a seguinte equação é obtida
Isto pode ser considerado como uma condição para o produto de modo transversal e parte da sua definição, por exemplo, em sete dimensões .